Les régulateurs à air ont été utilisés dans le passé particulièrement sur des mécanismes de types horloger, tournebroche mécanique et boîte à musique.
 |
 |
Le principe du régulateur est simple, il utilise le frottement de l'air sur des plaques planes animées d'un mouvement de rotation.
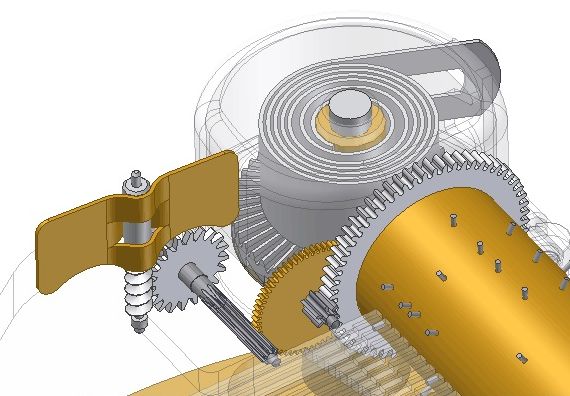 |
Compte tenu de la faible masse volumique de l'air, ces régulateurs ne peuvent, en action directe, que contrecarrer des couples moteurs faibles, et c'est en fait ce qui nous arrange.
--> En s'inspirant de ce principe, on peut fabriquer un dispositif simple pour tester nos moteurs neufs en charge. Cela évite les essais à vide, sans grand intérêt, et qui risquent endommager nos petites mécaniques compte tenu des vitesses atteintes ; en effet le moteur tourne très vite car n'ayant à compenser que ses frottements internes, c'est à dire pas grand chose s'il est bien construit.
Point de fonctionnement du moteur avec son régulateur
--> Le point de fonctionnement d'un moteur se trouve à l'intersection de la courbe du couple moteur et de celle du couple résistant.
--> un moteur à vapeur a un couple (presque) indépendant de la vitesse de rotation de l'arbre du vilebrequin.
--> le couple résistant dû à la traînée de l'air sur la palette est sensiblement proportionnel au carré de la somme1 de la vitesse de l'air et de la vitesse de déplacement de la palette.
Sur le diagramme ci-dessous on voit la forme parabolique de la résistance causée par la traînée des palettes dans l'air lors de leur rotation.
Omega est la vitesse de rotation de l'arbre moteur. On l'exprime en radians/seconde.
1 radian par seconde = 60/2/Pi=9,549 trs/mn ; 100 rds/s=954,9 trs/mn
Si on alimente le moteur à une pression P1 il va avoir un couple C1, par exemple 1000 sur l'exemple fictif du diagramme ; si cette pression augmente à P2 on aura un couple C2, par exemple 4000.
A l'examen on note qu'il y a deux points de fonctionnement :
- pour la pression C1 vers 50 rds/s soit environ 478 trs/mn
- pour la pression C2 vers 100 rds/s soit environ 955 trs/mn
On voit, sur cet exemple fictif, que pour un couple multiplié par 4 la vitesse n'est multipliée par que par 2.
Mieux si le couple était multiplié par 8, soit 8000 par rapport à C1, le point de fonctionnement se situerait vers 140 rds/s soit 1336 trs/mn pour autant que le régulateur ait été dimensionné pour fournir ce couple résistant. Dans ce cas la vitesse ne serait multipliée que par 140/50= 2,8.
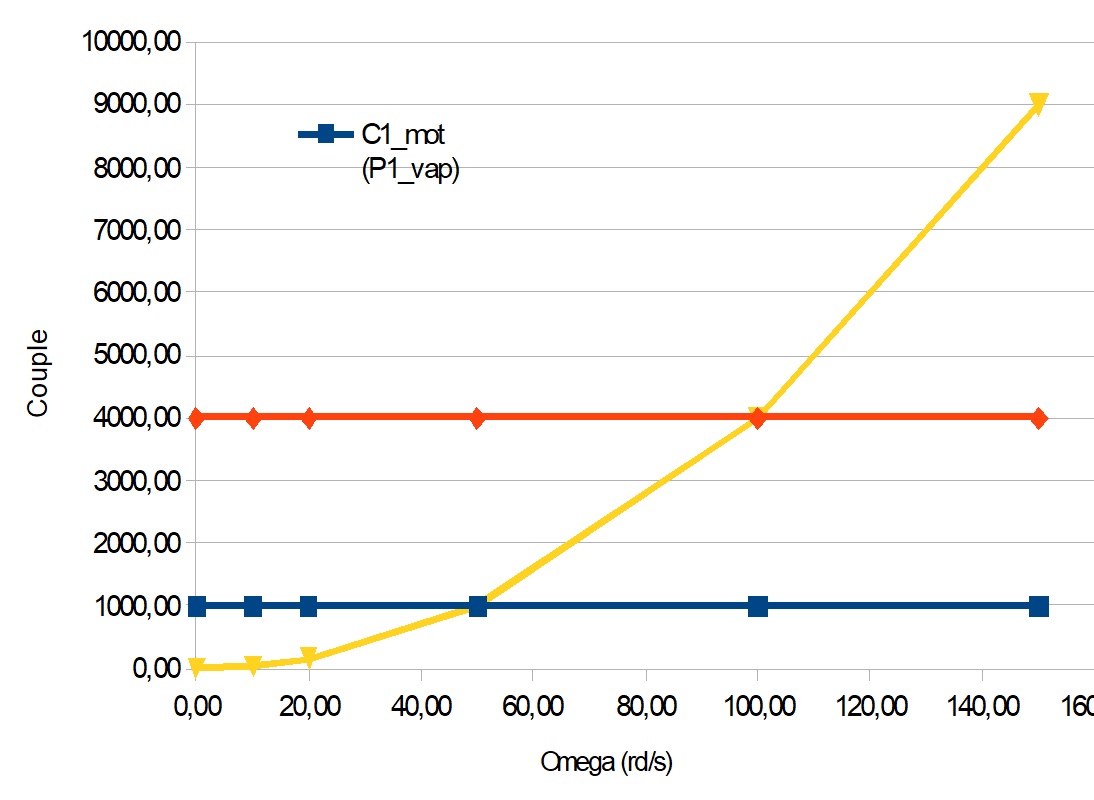 |
--> si la pression fluctue entre P1 et P2 la vitesse restera comprise dans des bornes acceptables, même pour des variations importantes. L'effet de « régulation » (On devrait plutôt parler de stabilité de fonctionnement) est lié à la forme des courbes.
Exemple de dispositif :
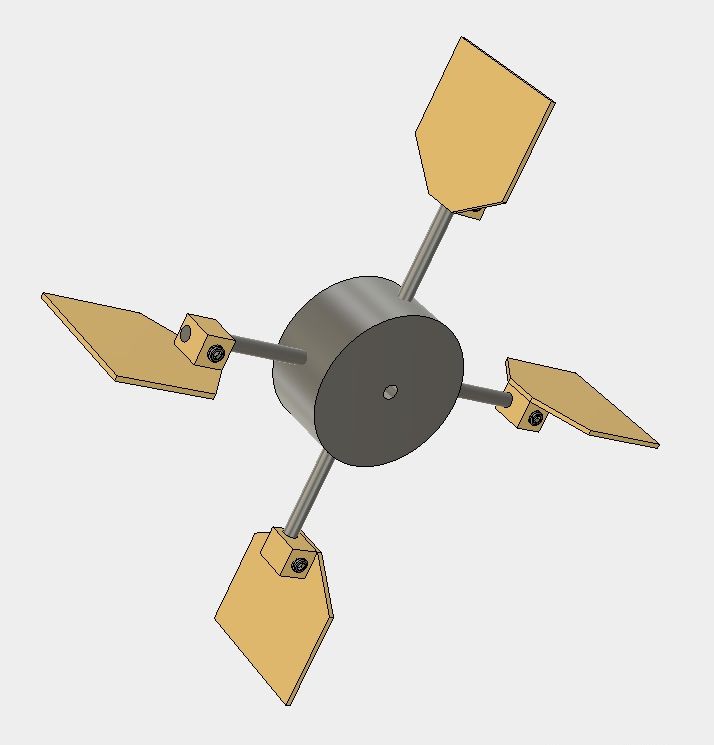 |
Il n'est pas nécessaire de faire de longs commentaires pour comprendre. Sur un volant d'inertie on visse 4 rayons, ou plus si on le souhaite. Sur ces rayons on place des palettes amovibles et réglables qui vont jouer le rôle de frein aérodynamique. On notera que les rayons apportent assez peu de traînée et ce sont les palettes qui font l'essentiel du travail résistant.
--> On a un dispositif assez versatile puisque l'on peut jouer sur la longueur de rayons, la taille et la position des palettes.
Estimation de la puissance mécanique nette
En l'absence d'étalonnage et moyennant quelques compromis de calcul on peut quand même, grâce à ce dispositif, avoir une estimation de la puissance mécanique nette du moteur.
Pour cela il nous faut connaître :
- la vitesse de rotation
- la force aérodynamique de traînée sur l'ensemble en mouvement
- l'endroit où s'applique cette force aérodynamique.
La ligne de conduite est :
- mesurer la vitesse de rotation Omega assez précisément car elle agit au carré de sa valeur
- calculer la force résistante aérodynamique F
- calculer le couple résistant Cr
- calculer la puissance Pr=Cr*Omega
- La puissance mécanique nette est égale en valeur absolue à Pr
 |
--> On voit que les facteurs sur lesquels on a toute latitude d'agir sont la surface de la palette et sa distance par rapport à l'axe de rotation
- La masse volumique de l'air rhô dans les conditions ordinaires tourne autour de 1,23 kg/m3. On trouve facilement des formules pour corriger l'effet de la température et de l'humidité, mais comme on est dans le domaine de l'estimation ce raffinement n'est peut-être pas nécessaire.
- Cx est un coefficient aérodynamique ; en général on prend une valeur de 1,1 pour une plaque plane et 0,4 pour un cylindre
- S est la surface de référence qui est perpendiculaire à l'écoulement du fluide. unité=m²
- V est la vitesse de déplacement en m/s. Comme la palette est en rotation, il s'agit de sa vitesse tangentielle. Elle s'exprime par V= R * Omega ; R est la distance à l'axe de rotation en mètre et omega la vitesse de rotation en radians/s.
La vitesse V varie donc tout le long de la palette . Il faut user que quelques ruses simples pour prendre cela en compte. Les palettes n'étant pas très longues, au pire on pourrait prendre la vitesse moyenne au centre de la plaque mais il vaut quand même mieux faire un calcul un peu plus correct.
Le plus simple est d'utiliser un petit outil ad'hoc développé sur tableur. ici
De ce qui précède on retiendra :
- doubler la surface de la palette double la force résistante
- doubler la distance du centre de la palette par rapport à l'axe de rotation quadruple la force résistante.
Test et réalisation du régulateur à air par Jacques CLABAUX : ici

